第2周:卷积神经网络
引言
本周学习视频为“02-卷积神经网络”,下载链接为:https://www.jianguoyun.com/p/Dde3HS8QrKKIBhi2xpEGIAA
1、视频学习
学习视频:卷积神经网络,主要内容包括:
- CNN的基本结构:卷积、池化、全连接
- 典型的⽹络结构:AlexNet、VGG、GoogleNet、ResNet
2、代码练习
实验1:使用LeNet对MNIST数据集分类
构建LeNet对 MNIST 数据集分类,实验指导在第4.1节。
要求:把代码输入 colab,在线运行观察效果。
实验2:使用参数接近的MLP和CNN分别对MNIST数据集分类
构建简单的CNN对 mnist 数据集进⾏分类。实验指导在第4.2节。
要求:把代码输入 colab,在线运行观察效果。
实验3:VGG16对CIFAR10分类
使⽤ VGG16 对 CIFAR10 分类,实验指导在第4.3节
要求:把代码输入 colab,在线运行观察效果。
实验4:ResNet18对CIFAR10分类
使⽤ ResNet18 对 CIFAR10 分类,实验指导在第4.4节
要求:把代码输入 colab,在线运行观察效果。
3、博客作业
完成一篇博客,思考下面的问题:
- dataloader 里面 shuffle 取不同值有什么区别?
- transform 里,取了不同值,这个有什么区别?
- epoch 和 batch 的区别?
- 1x1的卷积和 FC 有什么区别?主要起什么作⽤?
如果还有其它问题,可以总结一下,写在博客里,下周一起讨论。
4、实验环节
4.1 实验1:使用 LeNet 对 MNIST 数据集分类
下面的代码为使用 LeNet 进行 MNIST数据分类,使用豆包生成代码。
MNIST(Modified National Institute of Standards and Technology database)是深度学习和机器学习领域最经典的手写数字识别数据集,常被用作算法入门的 “Hello World” 级基准数据集,广泛应用于图像分类模型的性能验证与教学演示。
MNIST 数据集由美国国家标准与技术研究院(NIST)的原始手写数字数据修改而来,由 Yann LeCun 团队整理发布,其核心构成如下:
- 训练集:包含 60,000 张 28×28 像素的灰度手写数字图像,数据来源为美国人口普查局员工的手写样本;
- 测试集:包含 10,000 张同规格的灰度图像,数据来源为美国高中生的手写样本,用于独立验证模型泛化能力;
- 标签:每张图像对应一个 0-9 的数字标签,即 10 个分类类别,标签格式为整数型,可直接用于监督学习。
图像规格: 统一为 28×28 单通道灰度图,像素值范围为 0(黑色背景)到 255(白色数字),预处理时通常会归一化至 0-1 区间。
数据分布: 10 个数字类别在训练集和测试集中分布相对均衡,无严重的类别不平衡问题。
数据特点: 图像背景为纯色,数字区域轮廓清晰,但存在一定的手写风格差异(如数字 “4” 的开口方向、“9” 和 “6” 的混淆性),具备基础的分类挑战性。
第一步:配置基础参数
# 第一步:配置基础参数
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
# 设置设备:优先使用GPU,没有则用CPU
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 超参数
batch_size = 64
learning_rate = 0.001
num_epochs = 10深度学习的模型训练中,Epoch(中文常译 “轮次”) 是描述训练过程的基础单位,核心定义是:一个 Epoch 表示模型完整遍历了训练数据集的所有样本一次。
结合MNIST 数据集(训练集 60000 张图片),可以更直观理解:
- 核心逻辑(以 MNIST 为例): 当训练设置为 1 Epoch 时,模型会依次处理训练集中的全部 60000 张图片,完成一次 “从头到尾” 的遍历; 当设置为 10 Epochs 时,模型会把这 60000 张图片完整过 10 遍,即总共处理 60000×10 = 600000 张样本(重复使用训练集)。
- 为什么需要多个 Epochs? 模型的参数(如神经网络的权重)无法通过 “看一遍数据” 就达到最优,需要反复学习数据中的规律:第 1 个 Epoch:模型对数据规律的认知很浅,预测准确率低;后续 Epochs:模型通过反向传播不断调整参数,逐步拟合数据特征,准确率会提升。
与 Batch 的区别(新手必分清): 训练时很少一次性把所有数据喂给模型(内存不足),会把数据集拆成批次(Batch),两者的关系:
| 概念 | 定义 | 举例(MNIST,Batch Size=100) |
|---|---|---|
| Epoch | 遍历完整训练集 1 次 | 1 Epoch = 60000 张图片 |
| Batch Size | 每一批次喂给模型的样本数 | 1 Batch = 100 张图片 |
关键注意事项:
- Epoch 数不是越多越好:过多会导致模型 “过拟合”(只记住训练集,对测试集预测差); -早停(Early Stopping):训练时监控测试集准确率,当准确率不再提升甚至下降时,提前停止训练,避免过拟合;
- 常见取值:MNIST 这类简单数据集,Epoch 数通常设为 10、20、50;复杂数据集(如 ImageNet)可能需要上百个 Epochs(结合学习率衰减等策略)。
第二步:数据预处理和加载
# 定义数据变换:转为张量 + 归一化(MNIST均值和标准差)
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # MNIST数据集的统计值
])
# 加载MNIST数据集
train_dataset = datasets.MNIST(
root='./data', train=True, download=True, transform=transform
)
test_dataset = datasets.MNIST(
root='./data', train=False, download=True, transform=transform
)
# 创建数据加载器
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)transforms.Compose会把多个变换操作按顺序串联执行:
transforms.ToTensor() 作用是:① 将原始的图像数据(形状:28×28,像素值 0-255)转为 PyTorch 张量; ② 张量形状变为 (通道数, 高, 宽)(MNIST 是单通道,即(1, 28, 28)); ③ 像素值从 0-255 归一化到 0.0-1.0(除以 255)。
transforms.Normalize 作用是:对张量做归一化,公式:output = (input - mean) / std;
- (0.1307,):MNIST 训练集所有像素的均值(单通道所以是 1 个值);
- (0.3081,):MNIST 训练集所有像素的标准差;
✅ 作用:让数据分布更接近标准正态分布(均值 0,方差 1),加速模型收敛,提升训练稳定性。这里 0.1307 和 0.3081 是 MNIST 数据集的全局统计值(行业通用),无需自己计算,直接用即可。
DataLoader 里的 batch_size 是每一批次的样本数(比如batch_size=64,即一次喂给模型 64 张图片 + 64 个标签)。
shuffle : 训练集设置shuffle=True:每个 Epoch 开始时,随机打乱训练集的样本顺序;✅ 作用:避免模型学习到 “样本顺序” 的无关规律,提升泛化能力。 ❌ 测试集shuffle=False:测试时无需打乱,按顺序验证即可。
第三步:定义 LeNet-5 网络结构
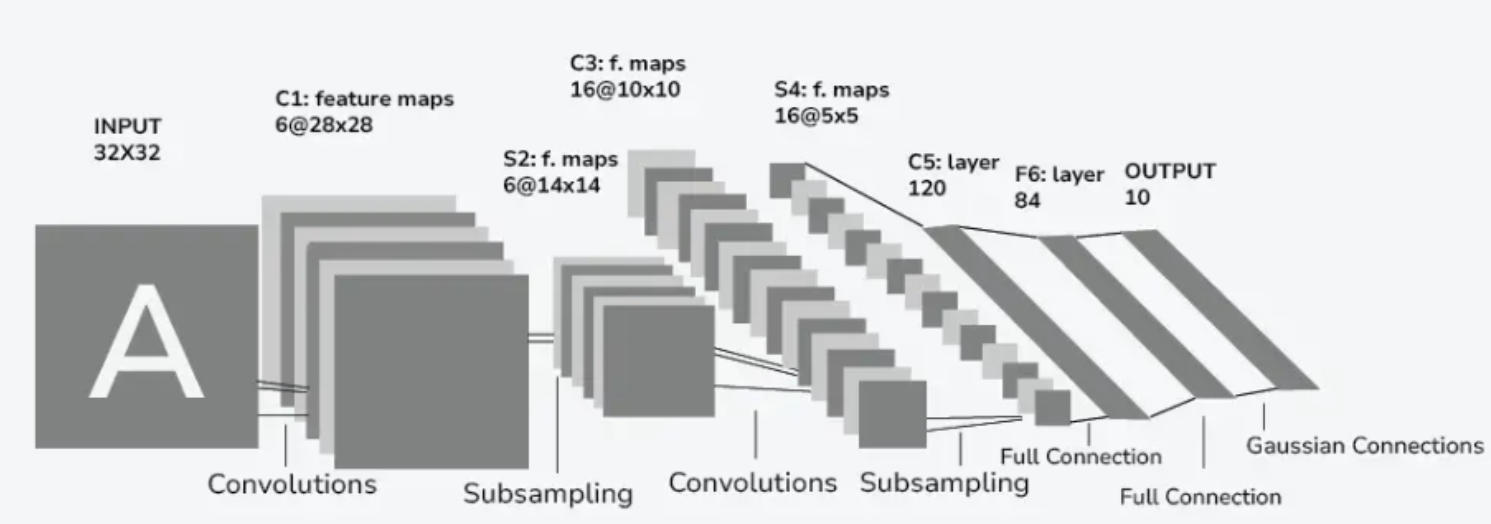
原始的 LeNet-5 结构如上图所示。不过对于 MNIST 数据集,输入是28x28,不是32x32,所以在第一个卷积里加了一个 padding,这样在第一次卷积后,feature map 的宽高就是28x28了。
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
# 卷积层:输入1通道(灰度图),输出6通道,卷积核5x5
self.conv1 = nn.Conv2d(1, 6, kernel_size=5, padding=2) # padding保证输出尺寸不变
self.relu1 = nn.ReLU()
self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2) # 池化核2x2,步长2
# 第二层卷积:输入6通道,输出16通道,卷积核5x5
self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
self.relu2 = nn.ReLU()
self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
# 全连接层:展平后维度16*5*5=400,输出120
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.relu3 = nn.ReLU()
# 第二层全连接:120->84
self.fc2 = nn.Linear(120, 84)
self.relu4 = nn.ReLU()
# 输出层:84->10(对应10个数字类别)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# 前向传播
# print("input: ", x.shape)
x = self.conv1(x)
# print("shape after conv1: ", x.shape)
x = self.pool1(self.relu1(x))
# print("shape after pool1: ", x.shape)
x = self.conv2(x)
# print("shape after conv2: ", x.shape)
x = self.pool2(self.relu2(x))
# print("shape after pool2: ", x.shape)
# 展平卷积层输出
x = x.view(-1, 16 * 5 * 5)
# print("shape after reshape:", x.shape)
x = self.relu3(self.fc1(x))
# print("shape after fc1:", x.shape)
x = self.relu4(self.fc2(x))
# print("shape after fc2:", x.shape)
x = self.fc3(x)
# print("shape after fc3:", x.shape)
return x下面代码为写一个随机矩阵来测试这个网络:
# 创建LeNet5模型实例
model = LeNet5()
# 用randn模拟标准化后的数据
random_input = torch.randn(4, 1, 28, 28)
# 前向传播
output = model(random_input)
# 输出结果说明
print("\n=== 测试结果 ===")
print(f"输入随机矩阵形状: {random_input.shape}")
print(f"网络输出形状: {output.shape}")注意到,上面的网络中 forward 部分有一些 print 语句备注掉了。如果不备注这些代码,测试网络可以得到下面的输出:
input: torch.Size([4, 1, 28, 28])
shape after conv1: torch.Size([4, 6, 28, 28])
shape after pool1: torch.Size([4, 6, 14, 14])
shape after conv2: torch.Size([4, 16, 10, 10])
shape after pool2: torch.Size([4, 16, 5, 5])
shape after reshape: torch.Size([4, 400])
shape after fc1: torch.Size([4, 120])
shape after fc2: torch.Size([4, 84])
shape after fc3: torch.Size([4, 10])
=== 测试结果 ===
输入随机矩阵形状: torch.Size([4, 1, 28, 28])
网络输出形状: torch.Size([4, 10])第四步:初始化模型、损失函数、优化器
model = LeNet5().to(device) # 将模型移到指定设备
criterion = nn.CrossEntropyLoss() # 交叉熵损失(适用于分类)
optimizer = optim.Adam(model.parameters(), lr=learning_rate) # Adam优化器这段代码是深度学习模型训练的核心配置三步曲:指定模型运行设备、定义损失函数、配置优化器,三者共同构成模型训练的基础框架。
为什么要移设备?
GPU 的并行计算能力远超 CPU,训练 MNIST 虽然简单,但 GPU 能让训练速度提升几十倍;注意:输入数据必须和模型在同一设备上(后续训练时,图片 / 标签也要.to(device),否则会报设备不匹配错误)。
Adam优化器的关键细节
optim.Adam(...):选择 Adam 优化器(目前深度学习最常用的优化器,兼顾效率和稳定性),替代传统的 SGD(随机梯度下降);model.parameters():传入模型所有可训练参数(LeNet5 的 conv1/conv2/fc1/fc2/fc3 的权重和偏置),优化器只更新这些参数;lr=learning_rate:学习率(超参数),决定参数更新的 “步长”:lr过大:参数更新步长太大,损失会震荡不收敛(比如学过头);lr过小:训练速度极慢,需要更多 Epoch 才能收敛;- MNIST+LeNet5 场景下,
learning_rate通常设为0.001(1e-3),是 Adam 的经典默认值。
keyboard_arrow_down
Adam 优化器的优势(对比 SGD)
- 自动调整学习率(无需手动衰减);
- 对学习率的初始值不敏感,收敛速度远快于基础 SGD;
- 适合 MNIST 这类简单任务,也适配复杂网络。
第五步:定义训练函数
def train(model, train_loader, criterion, optimizer, epoch):
model.train() # 训练模式
running_loss = 0.0
correct = 0
total = 0
for batch_idx, (images, labels) in enumerate(train_loader):
images, labels = images.to(device), labels.to(device)
# 前向传播
outputs = model(images)
loss = criterion(outputs, labels)
# 反向传播和优化
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
optimizer.step() # 更新参数
# 统计损失和准确率
running_loss += loss.item()
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
# 每100个batch打印一次信息
if (batch_idx + 1) % 100 == 0:
print(f'Epoch [{epoch+1}/{num_epochs}], Step [{batch_idx+1}/{len(train_loader)}], '
f'Loss: {running_loss/100:.4f}, Accuracy: {100*correct/total:.2f}%')
running_loss = 0.0这段代码是LeNet5 训练 MNIST 的核心训练函数,实现了单轮 Epoch 内模型的训练、损失 / 准确率统计,以及训练过程的可视化打印。
for batch_idx, (images, labels) in enumerate(train_loader):
images, labels = images.to(device), labels.to(device)enumerate(train_loader):遍历train_loader时,同时返回批次索引(batch_idx) 和批次数据(images, labels);images, labels = images.to(device):将当前批次的图片和标签移到模型所在的设备(GPU/CPU),保证 “数据和模型在同一设备”(否则会报设备不匹配错误);- 举例:如果
batch_size=64,则images形状为(64, 1, 28, 28),labels形状为(64,)。
outputs = model(images) : 模型对当前批次的图片做预测,输出形状为(batch_size, 10)(10 个数字类别的原始得分)
loss = criterion(outputs, labels): 计算当前批次的交叉熵损失: ① 自动对outputs做 Softmax 转概率; ② 计算预测概率与真实标签的交叉熵; ③ 返回的loss是标量张量(包含梯度信息);
# 反向传播和优化
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
optimizer.step() # 更新参数optimizer.zero_grad() 清空优化器中所有参数的梯度(PyTorch 梯度会累加,若不清空,会导致梯度错误)
loss.backward() 反向传播:从损失值出发,计算模型所有可训练参数的梯度(比如 conv1 的权重梯度、fc1 的偏置梯度)
optimizer.step() 优化器根据计算出的梯度,更新模型参数(Adam 会按学习率调整步长)
再后面:
| 代码行 | 作用详解 |
|---|---|
running_loss += loss.item() | 累加当前批次的损失值:① loss是张量,item()提取其标量值(避免占用计算图内存);② 累计到running_loss,用于后续计算 100 批次的平均损失; |
_, predicted = torch.max(outputs.data, 1) | 从模型输出中取预测类别:① outputs.data:取出输出张量(剥离梯度,节省资源);② torch.max(..., 1):在维度 1(类别维度)取最大值,返回(最大值, 索引);③ predicted是当前批次每个样本的预测类别(0-9); |
total += labels.size(0) | 累加总样本数:labels.size(0)是当前批次的样本数(即 batch_size); |
correct += (predicted == labels).sum().item() | 统计预测正确的样本数:① predicted == labels:逐元素比较,返回布尔张量;② .sum():统计 True 的数量(正确数);③ .item():转成 Python 整数累加; |
训练过程示例输出:
假设num_epochs=10,batch_size=64,输出类似:
Epoch [1/10], Step [100/938], Loss: 0.3254, Accuracy: 90.12%
Epoch [1/10], Step [200/938], Loss: 0.1021, Accuracy: 96.85%
...
Epoch [10/10], Step [900/938], Loss: 0.0089, Accuracy: 99.87%从输出能直观看到:随着训练推进,损失逐渐降低,准确率逐渐提升,说明模型在有效学习。
第六步: 定义测试函数
def test(model, test_loader, criterion):
model.eval() # 评估模式(关闭Dropout等)
test_loss = 0.0
correct = 0
total = 0
with torch.no_grad(): # 禁用梯度计算,节省内存和计算资源
for images, labels in test_loader:
images, labels = images.to(device), labels.to(device)
outputs = model(images)
loss = criterion(outputs, labels)
test_loss += loss.item()
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
avg_loss = test_loss / len(test_loader)
accuracy = 100 * correct / total
print(f'Test Loss: {avg_loss:.4f}, Test Accuracy: {accuracy:.2f}%\n')
return accuracy这段代码是模型评估(测试)函数,核心作用是在训练完成(或每轮 Epoch 训练后),用独立的测试集验证模型的泛化能力(即对未见过的数据的预测效果),输出测试集的平均损失和准确率,并返回准确率供后续分析(如早停、模型保存)。
with torch.no_grad()::上下文管理器,进入该上下文后,PyTorch 会禁用所有张量的梯度计算:
为什么必须加?
- 测试阶段不需要反向传播(无需计算梯度),禁用后可大幅节省 GPU/CPU 内存(梯度会占用大量内存);
- 加速前向传播(减少计算量);
- 避免意外修改模型梯度(保证模型参数不被测试过程干扰)。
关键设计原则:
| 维度 | 训练阶段(train 函数) | 测试阶段(test 函数) |
|---|---|---|
| 模型模式 | model.train() | model.eval() |
| 梯度计算 | 开启(需要反向传播更新参数) | 禁用(torch.no_grad()) |
| 核心操作 | 前向传播 + 损失计算 + 反向传播 + 参数更新 | 仅前向传播 + 损失计算(无参数更新) |
| 统计方式 | 每 100 批次打印一次进度 | 遍历完所有数据后计算整体指标 |
| 目的 | 让模型学习训练集规律 | 验证模型对未见过数据的泛化能力 |
第七步:执行训练和测试
best_accuracy = 0.0
for epoch in range(num_epochs):
train(model, train_loader, criterion, optimizer, epoch)
current_accuracy = test(model, test_loader, criterion)
# 保存最优模型
if current_accuracy > best_accuracy:
best_accuracy = current_accuracy
torch.save(model.state_dict(), 'lenet_mnist_best.pth')
print(f'Best Test Accuracy: {best_accuracy:.2f}%')这段代码是LeNet5 训练 MNIST 的核心主循环,实现了「多轮 Epoch 训练→每轮测试→保存最优模型→输出最终最优准确率」的完整流程,是深度学习训练中 “持续验证 + 模型择优” 的经典范式。
整体逻辑:先初始化 “最优准确率” 为 0,然后逐轮执行:训练1轮 → 测试1轮 → 对比当前测试准确率与历史最优 → 若更优则保存模型。
最终输出训练过程中达到的最高测试准确率,确保我们保留泛化能力最强的模型。
关键设计思路
1. 为什么不保存最后一轮的模型?
训练过程中,模型性能通常是 “提升→峰值→下降” 的趋势(过拟合):
- 前几轮:模型学习训练集规律,测试准确率逐步提升;
- 峰值轮:测试准确率达到最高(泛化能力最强);
- 后续轮:模型开始 “死记” 训练集(过拟合),训练准确率继续提升,但测试准确率下降。
如果只保存最后一轮的模型,大概率是过拟合的模型;而保存 “最优准确率” 对应的模型,能拿到泛化能力最好的版本。
2. model.state_dict()的优势
- 轻量:仅保存参数(LeNet5 的参数文件约几百 KB),而非整个模型类;
- 灵活:后续加载时,只需重新定义 LeNet5 类,再加载参数即可:
- 可移植:参数文件可跨环境使用(比如在训练机保存,在推理机加载)。
不依赖 “最后一轮”,而是通过持续验证选择泛化能力最强的模型,这是避免过拟合、保证模型实际可用的关键步骤。 对于 MNIST 这类简单任务,该逻辑能稳定拿到 98%+ 的最优准确率;对于复杂任务(如 ImageNet),这一范式更是必不可少。
4.2 实验2:使用参数接近的MLP和CNN分别对MNIST数据集分类
Outline
今天我们学习如何使用 PyTorch 进行CNN的训练与测试
我们还会展示池化与卷积操作的作用
深度卷积神经网络中,有如下特性
很多层: compositionality
卷积: locality + stationarity of images
池化: Invariance of object class to translations
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import numpy
# 一个函数,用来计算模型中有多少参数def get_n_params(model):
np=0for p in list(model.parameters()):
np += p.nelement()
return np
# 使用GPU训练,可以在菜单 "代码执行工具" -> "更改运行时类型" 里进行设置
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")第一步: 加载数据 (MNIST)
PyTorch里包含了 MNIST, CIFAR10 等常用数据集,调用 torchvision.datasets 即可把这些数据由远程下载到本地,下面给出MNIST的使用方法:
torchvision.datasets.MNIST(root, train=True, transform=None, target_transform=None, download=False)
- root 为数据集下载到本地后的根目录,包括 training.pt 和 test.pt 文件
- train,如果设置为True,从training.pt创建数据集,否则从test.pt创建。
- download,如果设置为True, 从互联网下载数据并放到root文件夹下
- transform, 一种函数或变换,输入PIL图片,返回变换之后的数据。
- target_transform 一种函数或变换,输入目标,进行变换。
另外值得注意的是,DataLoader是一个比较重要的类,提供的常用操作有:batch_size(每个batch的大小), shuffle(是否进行随机打乱顺序的操作), num_workers(加载数据的时候使用几个子进程)
input_size = 28*28 # MNIST上的图像尺寸是 28x28
output_size = 10 # 类别为 0 到 9 的数字,因此为十类
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('./data', train=True, download=True,
transform=transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))])),
batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('./data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))])),
batch_size=1000, shuffle=True)显示数据集中的部分图像
plt.figure(figsize=(8, 5))
for i in range(20):
plt.subplot(4, 5, i + 1)
image, _ = train_loader.dataset.__getitem__(i)
plt.imshow(image.squeeze().numpy(),'gray')
plt.axis('off');
第二步:创建网络
定义网络时,需要继承nn.Module,并实现它的forward方法,把网络中具有可学习参数的层放在构造函数__init__中。
只要在nn.Module的子类中定义了forward函数,backward函数就会自动被实现(利用autograd)。
class FC2Layer(nn.Module):def __init__(self, input_size, n_hidden, output_size):
# nn.Module子类的函数必须在构造函数中执行父类的构造函数# 下式等价于nn.Module.__init__(self)
super(FC2Layer, self).__init__()
self.input_size = input_size
# 这里直接用 Sequential 就定义了网络,注意要和下面 CNN 的代码区分开
self.network = nn.Sequential(
nn.Linear(input_size, n_hidden),
nn.ReLU(),
nn.Linear(n_hidden, n_hidden),
nn.ReLU(),
nn.Linear(n_hidden, output_size),
nn.LogSoftmax(dim=1)
)
def forward(self, x):
# view一般出现在model类的forward函数中,用于改变输入或输出的形状
# x.view(-1, self.input_size) 的意思是多维的数据展成二维
# 代码指定二维数据的列数为 input_size=784,行数 -1 表示我们不想算,
# 电脑会自己计算对应的数字
# 在 DataLoader 部分,我们可以看到 batch_size 是64,所以得到 x 的行数是64
# 大家可以加一行代码:print(x.cpu().numpy().shape)
# 训练过程中,就会看到 (64, 784) 的输出,和我们的预期是一致的
# forward 函数的作用是,指定网络的运行过程,这个全连接网络可能看不啥意义
# 下面的CNN网络可以看出 forward 的作用。
x = x.view(-1, self.input_size)
return self.network(x)
class CNN(nn.Module):def __init__(self, input_size, n_feature, output_size):
# 执行父类的构造函数,所有的网络都要这么写
super(CNN, self).__init__()
# 下面是网络里典型结构的一些定义,一般就是卷积和全连接
# 池化、ReLU一类的不用在这里定义
self.n_feature = n_feature
self.conv1 = nn.Conv2d(in_channels=1, out_channels=n_feature, kernel_size=5)
self.conv2 = nn.Conv2d(n_feature, n_feature, kernel_size=5)
self.fc1 = nn.Linear(n_feature*4*4, 50)
self.fc2 = nn.Linear(50, 10)
# 下面的 forward 函数,定义了网络的结构,按照一定顺序,把上面构建的一些结构组织起来
# 意思就是,conv1, conv2 等等的,可以多次重用
def forward(self, x, verbose=False):
x = self.conv1(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2)
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2)
x = x.view(-1, self.n_feature*4*4)
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = F.log_softmax(x, dim=1)
return x定义训练和测试函数
# 训练函数def train(model):
model.train()
# 主里从train_loader里,64个样本一个batch为单位提取样本进行训练
for batch_idx, (data, target) in enumerate(train_loader):
# 把数据送到GPU中
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % 100 == 0:
print('Train: [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
def test(model):
model.eval()
test_loss = 0
correct = 0for data, target in test_loader:
# 把数据送到GPU中
data, target = data.to(device), target.to(device)
# 把数据送入模型,得到预测结果
output = model(data)
# 计算本次batch的损失,并加到 test_loss 中
test_loss += F.nll_loss(output, target, reduction='sum').item()
# get the index of the max log-probability,最后一层输出10个数
# 值最大的那个即对应着分类结果,然后把分类结果保存在 pred 里
pred = output.data.max(1, keepdim=True)[1]
# 将 pred 与 target 相比,得到正确预测结果的数量,并加到 correct 中
# 这里需要注意一下 view_as ,意思是把 target 变成维度和 pred 一样的意思
correct += pred.eq(target.data.view_as(pred)).cpu().sum().item()
test_loss /= len(test_loader.dataset)
accuracy = 100. * correct / len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
accuracy))第三步:在小型全连接网络上训练(Fully-connected network)
n_hidden = 8
# number of hidden units
model_fnn = FC2Layer(input_size, n_hidden, output_size)
model_fnn.to(device)
optimizer = optim.SGD(model_fnn.parameters(), lr=0.01, momentum=0.5)
print('Number of parameters: {}'.format(get_n_params(model_fnn)))
train(model_fnn)
test(model_fnn)Number of parameters: 6442
Train: [0/60000 (0%)] Loss: 2.302146
Train: [6400/60000 (11%)] Loss: 1.951977
Train: [12800/60000 (21%)] Loss: 1.290410
Train: [19200/60000 (32%)] Loss: 1.000708
Train: [25600/60000 (43%)] Loss: 0.829704
Train: [32000/60000 (53%)] Loss: 0.553799
Train: [38400/60000 (64%)] Loss: 0.596026
Train: [44800/60000 (75%)] Loss: 0.720949
Train: [51200/60000 (85%)] Loss: 0.557444
Train: [57600/60000 (96%)] Loss: 0.593830
Test set: Average loss: 0.4253, Accuracy: 8735/10000 (87%)
第四步:在卷积神经网络上训练
需要注意的是,上在定义的CNN和全连接网络,拥有相同数量的模型参数
# number of feature maps
n_features = 6
model_cnn = CNN(input_size, n_features, output_size)
model_cnn.to(device)
optimizer = optim.SGD(model_cnn.parameters(), lr=0.01, momentum=0.5)
print('Number of parameters: {}'.format(get_n_params(model_cnn)))
train(model_cnn)
test(model_cnn)Number of parameters: 6422
Train: [0/60000 (0%)] Loss: 2.328946
Train: [6400/60000 (11%)] Loss: 1.301481
Train: [12800/60000 (21%)] Loss: 0.472606
Train: [19200/60000 (32%)] Loss: 0.415483
Train: [25600/60000 (43%)] Loss: 0.179762
Train: [32000/60000 (53%)] Loss: 0.350131
Train: [38400/60000 (64%)] Loss: 0.177829
Train: [44800/60000 (75%)] Loss: 0.121229
Train: [51200/60000 (85%)] Loss: 0.140334
Train: [57600/60000 (96%)] Loss: 0.333439
Test set: Average loss: 0.1266, Accuracy: 9615/10000 (96%)
通过上面的测试结果,可以发现,含有相同参数的 CNN 效果要明显优于 简单的全连接网络,是因为 CNN 能够更好的挖掘图像中的信息,主要通过两个手段:
- 卷积:Locality and stationarity in images
- 池化:Builds in some translation invariance
第五步:打乱像素顺序再次在两个网络上训练与测试
考虑到CNN在卷积与池化上的优良特性,如果我们把图像中的像素打乱顺序,这样 卷积 和 池化 就难以发挥作用了,为了验证这个想法,我们把图像中的像素打乱顺序再试试。
首先下面代码展示随机打乱像素顺序后,图像的形态:
# 这里解释一下 torch.randperm 函数,
# 给定参数n,返回一个从0到n-1的随机整数排列
perm = torch.randperm(784)
plt.figure(figsize=(8, 4))
for i in range(10):
image, _ = train_loader.dataset.__getitem__(i)
# permute pixels
image_perm = image.view(-1, 28*28).clone()
image_perm = image_perm[:, perm]
image_perm = image_perm.view(-1, 1, 28, 28)
plt.subplot(4, 5, i + 1)
plt.imshow(image.squeeze().numpy(), 'gray')
plt.axis('off')
plt.subplot(4, 5, i + 11)
plt.imshow(image_perm.squeeze().numpy(), 'gray')
plt.axis('off')
重新定义训练与测试函数,我们写了两个函数 train_perm 和 test_perm,分别对应着加入像素打乱顺序的训练函数与测试函数。
与之前的训练与测试函数基本上完全相同,只是对 data 加入了打乱顺序操作。
# 对每个 batch 里的数据,打乱像素顺序的函数
def perm_pixel(data, perm):
# 转化为二维矩阵
data_new = data.view(-1, 28*28)
# 打乱像素顺序
data_new = data_new[:, perm]
# 恢复为原来4维的 tensor
data_new = data_new.view(-1, 1, 28, 28)
return data_new
# 训练函数
def train_perm(model, perm):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
# 像素打乱顺序
data = perm_pixel(data, perm)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % 100 == 0:
print('Train: [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
# 测试函数
def test_perm(model, perm):
model.eval()
test_loss = 0
correct = 0for data, target in test_loader:
data, target = data.to(device), target.to(device)
# 像素打乱顺序
data = perm_pixel(data, perm)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).cpu().sum().item()
test_loss /= len(test_loader.dataset)
accuracy = 100. * correct / len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
accuracy))在全连接网络上训练与测试:
perm = torch.randperm(784)
n_hidden = 8 # number of hidden unitsmodel_fnn = FC2Layer(input_size, n_hidden, output_size)
model_fnn.to(device)
optimizer = optim.SGD(model_fnn.parameters(), lr=0.01, momentum=0.5)
print('Number of parameters: {}'.format(get_n_params(model_fnn)))
train_perm(model_fnn, perm)
test_perm(model_fnn, perm)Number of parameters: 6442
Train: [0/60000 (0%)] Loss: 2.264858
Train: [6400/60000 (11%)] Loss: 2.041490
Train: [12800/60000 (21%)] Loss: 1.552290
Train: [19200/60000 (32%)] Loss: 1.093537
Train: [25600/60000 (43%)] Loss: 0.799383
Train: [32000/60000 (53%)] Loss: 0.847221
Train: [38400/60000 (64%)] Loss: 0.756004
Train: [44800/60000 (75%)] Loss: 0.723714
Train: [51200/60000 (85%)] Loss: 0.438829
Train: [57600/60000 (96%)] Loss: 0.474032
Test set: Average loss: 0.5751, Accuracy: 8348/10000 (83%)
在卷积神经网络上训练与测试:
perm = torch.randperm(784)
# number of feature maps
n_features = 6
model_cnn = CNN(input_size, n_features, output_size)
model_cnn.to(device)
optimizer = optim.SGD(model_cnn.parameters(), lr=0.01, momentum=0.5)
print('Number of parameters: {}'.format(get_n_params(model_cnn)))
train_perm(model_cnn, perm)
test_perm(model_cnn, perm)Number of parameters: 6422
Train: [0/60000 (0%)] Loss: 2.300903
Train: [6400/60000 (11%)] Loss: 2.282535
Train: [12800/60000 (21%)] Loss: 2.261807
Train: [19200/60000 (32%)] Loss: 2.111837
Train: [25600/60000 (43%)] Loss: 1.717916
Train: [32000/60000 (53%)] Loss: 1.320999
Train: [38400/60000 (64%)] Loss: 0.960259
Train: [44800/60000 (75%)] Loss: 0.961738
Train: [51200/60000 (85%)] Loss: 0.636504
Train: [57600/60000 (96%)] Loss: 0.507474
Test set: Average loss: 0.6227, Accuracy: 8003/10000 (80%)
从打乱像素顺序的实验结果来看,全连接网络的性能基本上没有发生变化,但是 卷积神经网络的性能明显下降。
这是因为对于卷积神经网络,会利用像素的局部关系,但是打乱顺序以后,这些像素间的关系将无法得到利用。
4.3 实验3:使用VGG对CIFAR10分类
VGG是由Simonyan 和Zisserman在文献《Very Deep Convolutional Networks for Large Scale Image Recognition》中提出卷积神经网络模型,其名称来源于作者所在的牛津大学视觉几何组(Visual Geometry Group)的缩写。该模型参加2014年的 ImageNet图像分类与定位挑战赛,取得了优异成绩:在分类任务上排名第二,在定位任务上排名第一。
CIFAR10(Canadian Institute for Advanced Research)是深度学习领域最经典的图像分类基准数据集之一,由 Alex Krizhevsky、Vinod Nair 和 Geoffrey Hinton 整理发布,尤其适合入门级计算机视觉算法的训练与测试。CIFAR10 包含 60000 张 32×32 像素的彩色 RGB 图像,分为 50000 张训练集 + 10000 张测试集,图像分辨率较低,计算成本小,适合快速迭代模型。

第一步:定义 dataloader
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm
import os
# 使用GPU训练,可以在菜单 "代码执行工具" -> "更改运行时类型" 里进行设置
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# CIFAR10数据增强和预处理
transform_train = transforms.Compose([
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010))])
transform_test = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010))])
# 加载CIFAR10数据集
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform_train)
testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform_test)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True, num_workers=2)
testloader = torch.utils.data.DataLoader(testset, batch_size=128, shuffle=False, num_workers=2)
# CIFAR10类别名称
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')第二步:定义VGG网络
输入为32x32,所以手动将网络改简单了些,现在网络结构为:
64 conv, maxpooling,
128 conv, maxpooling,
256 conv, 256 conv, maxpooling,
512 conv, 512 conv, maxpooling,
512 conv, 512 conv, maxpooling,
softmax下面是模型的实现代码:
class VGG(nn.Module):
def __init__(self):
super(VGG, self).__init__()
self.cfg = [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M']
self.features = self._make_layers(self.cfg)
self.classifier = nn.Linear(512, 10)
def forward(self, x):
out = self.features(x)
out = out.view(out.size(0), -1) # 展平
out = self.classifier(out)
return out
def _make_layers(self, cfg):
layers = []
in_channels = 3 # 修复:原代码缺少换行,导致语法错误
for x in cfg:
if x == 'M':
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
else:
layers += [
nn.Conv2d(in_channels, x, kernel_size=3, padding=1),
nn.BatchNorm2d(x),
nn.ReLU(inplace=True)
]
in_channels = x
layers += [nn.AvgPool2d(kernel_size=1, stride=1)]
return nn.Sequential(*layers)初始化模型,定义损失函数和优化器:
# 初始化模型并移至设备
model = VGG().to(device)
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)第三步:定义训练函数和测试函数
# 训练函数
def train(model, trainloader, criterion, optimizer, epoch):
model.train()
running_loss = 0.0
correct = 0
total = 0
pbar = tqdm(enumerate(trainloader), total=len(trainloader), desc=f'Epoch {epoch}')
for batch_idx, (inputs, targets) in pbar:
inputs, targets = inputs.to(device), targets.to(device)
# 前向传播
outputs = model(inputs)
loss = criterion(outputs, targets)
# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 统计
running_loss += loss.item()
_, predicted = outputs.max(1)
total += targets.size(0)
correct += predicted.eq(targets).sum().item()
# 更新进度条
pbar.set_postfix({
'Loss': running_loss/(batch_idx+1),
'Acc': 100.*correct/total
})
return running_loss/len(trainloader), 100.*correct/total
# 测试函数
def test(model, testloader, criterion):
model.eval()
running_loss = 0.0
correct = 0
total = 0
with torch.no_grad(): # 禁用梯度计算
for inputs, targets in testloader:
inputs, targets = inputs.to(device), targets.to(device)
outputs = model(inputs)
loss = criterion(outputs, targets)
running_loss += loss.item()
_, predicted = outputs.max(1)
total += targets.size(0)
correct += predicted.eq(targets).sum().item()
test_loss = running_loss/len(testloader)
test_acc = 100.*correct/total
print(f'\nTest set: Average loss: {test_loss:.4f}, Accuracy: {correct}/{total} ({test_acc:.2f}%)\n')
return test_loss, test_acc第四步:主训练循环
epochs = 10
best_acc = 0.0
train_losses = []
train_accs = []
test_losses = []
test_accs = []
# 创建保存模型的目录
os.makedirs('./checkpoints', exist_ok=True)
for epoch in range(1, epochs+1):
train_loss, train_acc = train(model, trainloader, criterion, optimizer, epoch)
test_loss, test_acc = test(model, testloader, criterion)
# 记录指标
train_losses.append(train_loss)
train_accs.append(train_acc)
test_losses.append(test_loss)
test_accs.append(test_acc)
# 保存最佳模型
if test_acc > best_acc:
best_acc = test_acc
torch.save(model.state_dict(), './checkpoints/vgg_cifar10_best.pth')
print(f"保存最佳模型,准确率: {best_acc:.2f}%")第五步:结果可视化
plt.figure(figsize=(12, 4))
# 损失曲线
plt.subplot(1, 2, 1)
plt.plot(train_losses, label='Train Loss')
plt.plot(test_losses, label='Test Loss')
plt.title('Loss Curve')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
# 准确率曲线
plt.subplot(1, 2, 2)
plt.plot(train_accs, label='Train Acc')
plt.plot(test_accs, label='Test Acc')
plt.title('Accuracy Curve')
plt.xlabel('Epoch')
plt.ylabel('Accuracy (%)')
plt.legend()
plt.tight_layout()
plt.savefig('vgg_cifar10_results.png')
plt.show()第六步:加载最佳模型并测试
print(f"\n最佳测试准确率: {best_acc:.2f}%")
model.load_state_dict(torch.load('./checkpoints/vgg_cifar10_best.pth'))
final_test_loss, final_test_acc = test(model, testloader, criterion)
print(f"加载最佳模型后最终测试准确率: {final_test_acc:.2f}%")第七步:查看各类别准确率
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
model.eval()
with torch.no_grad():
for inputs, targets in testloader:
inputs, targets = inputs.to(device), targets.to(device)
outputs = model(inputs)
_, predicted = torch.max(outputs, 1)
c = (predicted == targets).squeeze()
for i in range(targets.size(0)):
label = targets[i]
class_correct[label] += c[i].item()
class_total[label] += 1
# 打印各类别准确率
for i in range(10):
print(f'Accuracy of {classes[i]} : {100 * class_correct[i] / class_total[i]:.2f}%')4.4 实验4:使用ResNet18对CIFAR10分类
训练和数据集的代码不变,只是网络上的代码有变化。首先定义BasicBlock类,如下图所示。
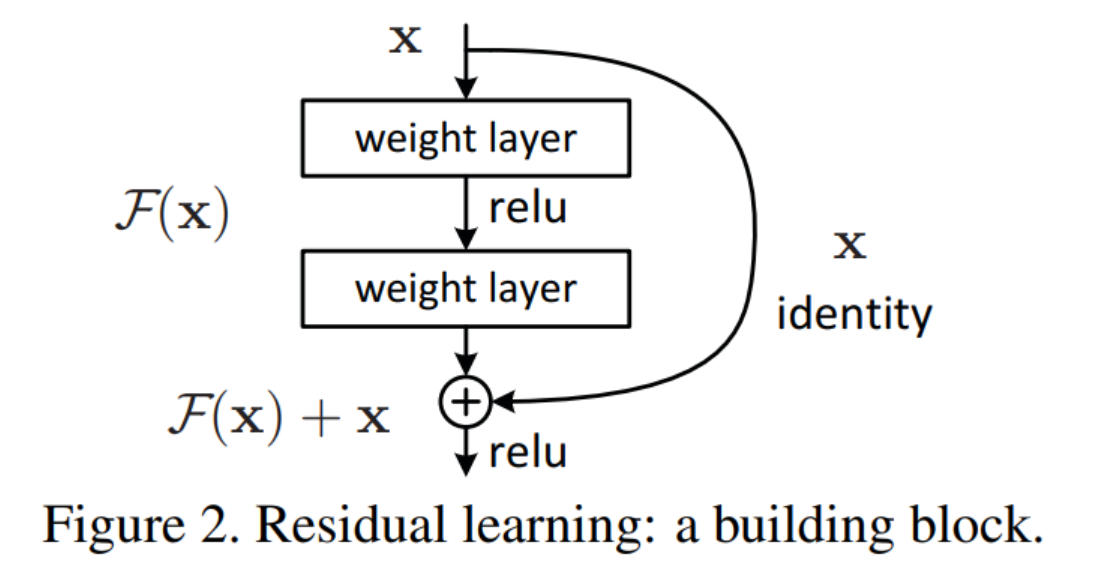
class BasicBlock(nn.Module):
"""ResNet的基本块(18/34层使用)"""
expansion = 1 # 通道扩展系数
def __init__(self, in_channels, out_channels, stride=1):
super(BasicBlock, self).__init__()
# 第一个卷积层
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3,
stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(out_channels)
# 第二个卷积层
self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3,
stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_channels)
# 捷径连接(shortcut):处理通道数/尺寸不匹配的情况
self.shortcut = nn.Sequential()
if stride != 1 or in_channels != self.expansion * out_channels:
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, self.expansion * out_channels,
kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion * out_channels)
)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
out += self.shortcut(x) # 残差连接
out = F.relu(out)
return outResNet 通过堆叠 “残差块” 构建网络,BasicBlock 是针对浅层 ResNet(18/34 层) 设计的基础残差块,特点是包含2 个 3×3 卷积层,且通道数扩展系数expansion=1(深层 ResNet 如 50/101 层用 Bottleneck 块,expansion=4)。
其核心思想是残差学习:不再让网络直接学习目标映射 H(x),而是学习残差映射 F(x)=H(x)−x,最终输出 H(x)=F(x)+x。这种设计解决了深层网络的梯度消失问题,让网络可以堆叠更多层。
在 self.shortcut 里,条件判断stride != 1 or in_channels != self.expansion * out_channels:当尺寸缩放(stride=2)或通道数不匹配时,需要用 1×1 卷积调整 shortcut 的维度:
kernel_size=1:1×1 卷积仅调整通道数,不改变空间信息;stride=stride:同步缩放尺寸(与 conv1 的 stride 一致);- 输出通道数
self.expansion * out_channels:匹配残差分支的输出通道数。
ResNet网络代码如下。ResNet类是通用的 ResNet 架构模板,支持传入不同的残差块(如BasicBlock)、不同数量的残差块堆叠数(num_blocks),从而灵活构建 ResNet18/34(用BasicBlock)、ResNet50/101(用Bottleneck)。
ResNet18函数是封装后的快捷方法,固定使用BasicBlock且堆叠数为[2,2,2,2],最终形成 18 层的 ResNet(1 个初始卷积 + 4 组残差层 ×2 个 BasicBlock + 1 个全连接层)。
class ResNet(nn.Module):
def __init__(self, block, num_blocks, num_classes=10):
super(ResNet, self).__init__()
self.in_channels = 64
# 初始卷积层(适配CIFAR10的32x32输入)
self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)
self.avgpool = nn.AdaptiveAvgPool2d((1, 1)) # 自适应平均池化
self.fc = nn.Linear(512 * block.expansion, num_classes)
def _make_layer(self, block, out_channels, num_blocks, stride):
strides = [stride] + [1]*(num_blocks-1)
layers = []
for stride in strides:
layers.append(block(self.in_channels, out_channels, stride))
self.in_channels = out_channels * block.expansion
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = self.avgpool(out)
out = torch.flatten(out, 1)
out = self.fc(out)
return out
def ResNet18(num_classes=10):
"""构建ResNet18模型"""
return ResNet(BasicBlock, [2, 2, 2, 2], num_classes)数据维度变化(以 CIFAR10 32×32 输入为例):
| 步骤 | 输入维度 | 操作 | 输出维度 |
|---|---|---|---|
| 初始卷积 + BN+ReLU | (B,3,32,32) | conv1(3→64) + BN1 + ReLU | (B,64,32,32) |
| layer1(2 个 BasicBlock) | (B,64,32,32) | 2×BasicBlock(64→64, stride=1) | (B,64,32,32) |
| layer2(2 个 BasicBlock) | (B,64,32,32) | 1×BasicBlock(64→128, stride=2) + 1×BasicBlock(128→128, stride=1) | (B,128,16,16) |
| layer3(2 个 BasicBlock) | (B,128,16,16) | 1×BasicBlock(128→256, stride=2) + 1×BasicBlock(256→256, stride=1) | (B,256,8,8) |
| layer4(2 个 BasicBlock) | (B,256,8,8) | 1×BasicBlock(256→512, stride=2) + 1×BasicBlock(512→512, stride=1) | (B,512,4,4) |
| 自适应平均池化 | (B,512,4,4) | AdaptiveAvgPool2d(1,1) | (B,512,1,1) |
| 展平 | (B,512,1,1) | torch.flatten(out,1) | (B,512) |
| 全连接层 | (B,512) | Linear(512→10) |
